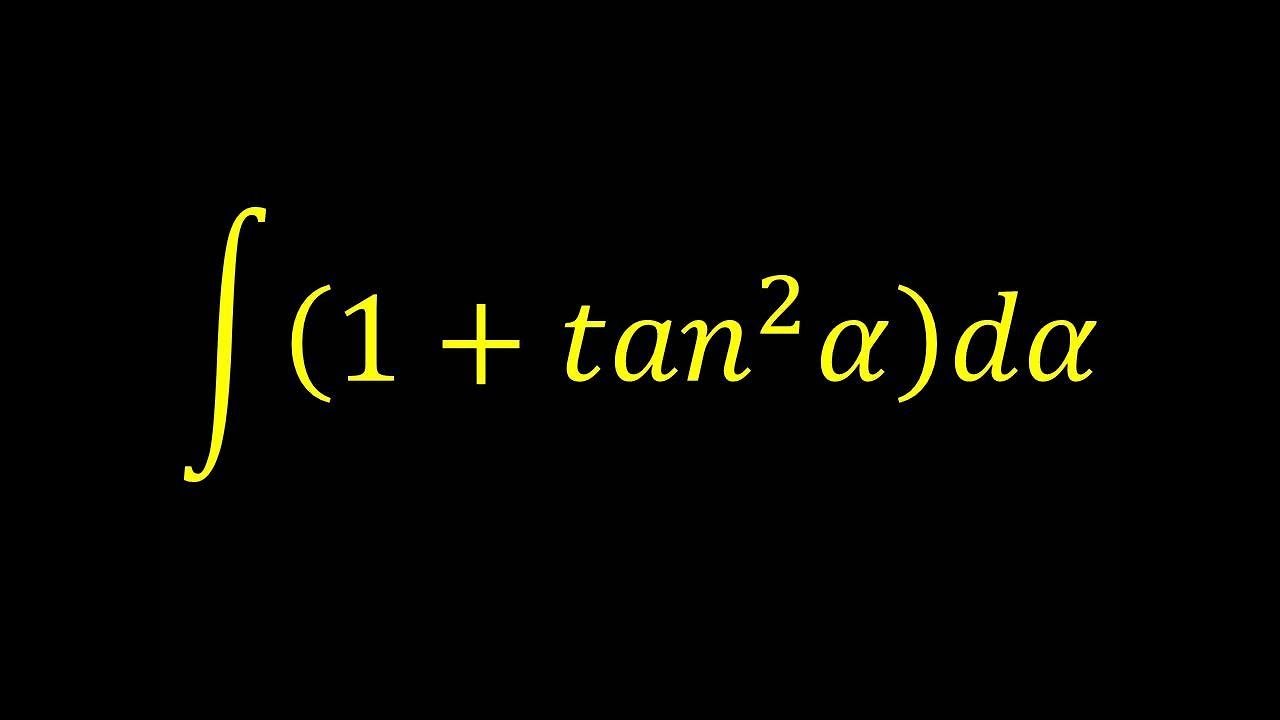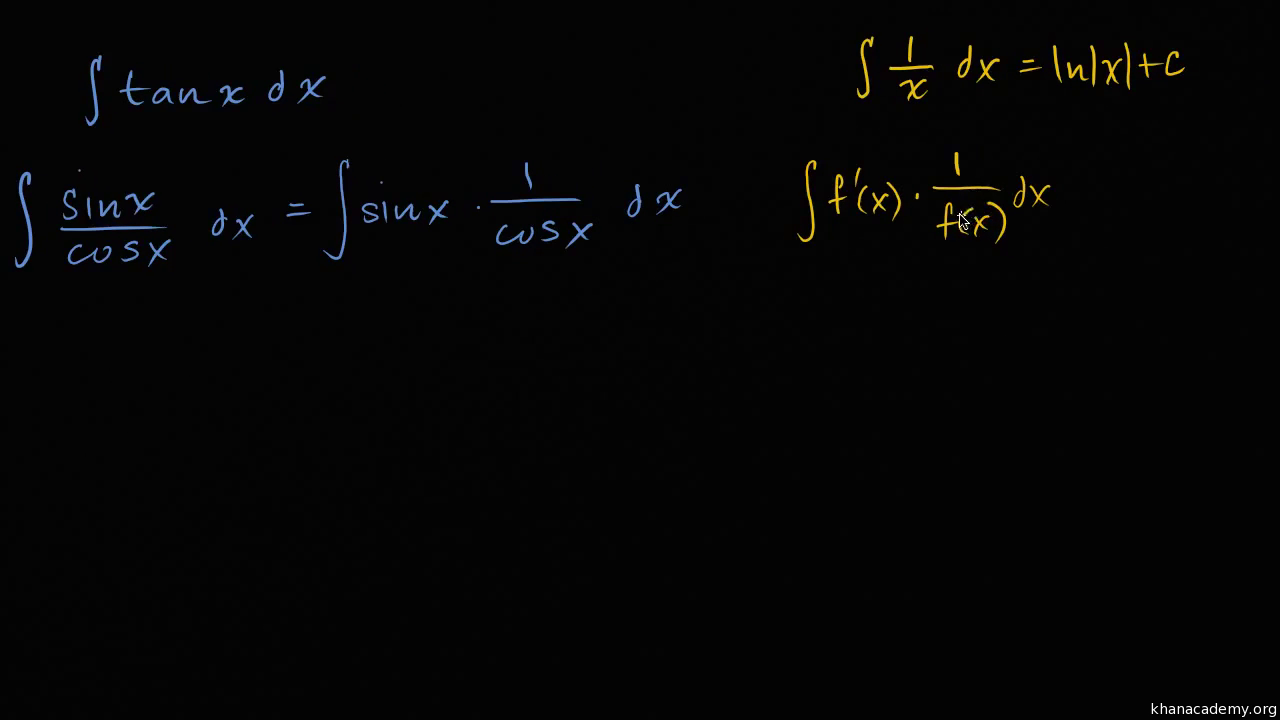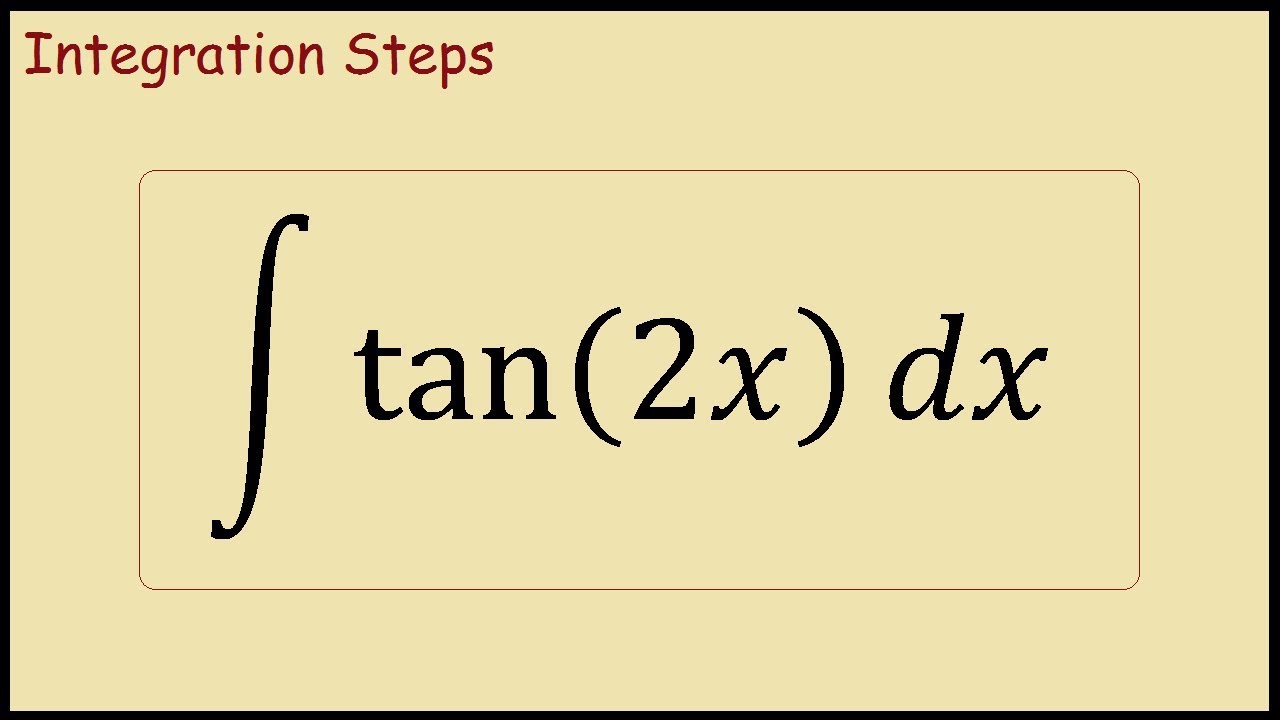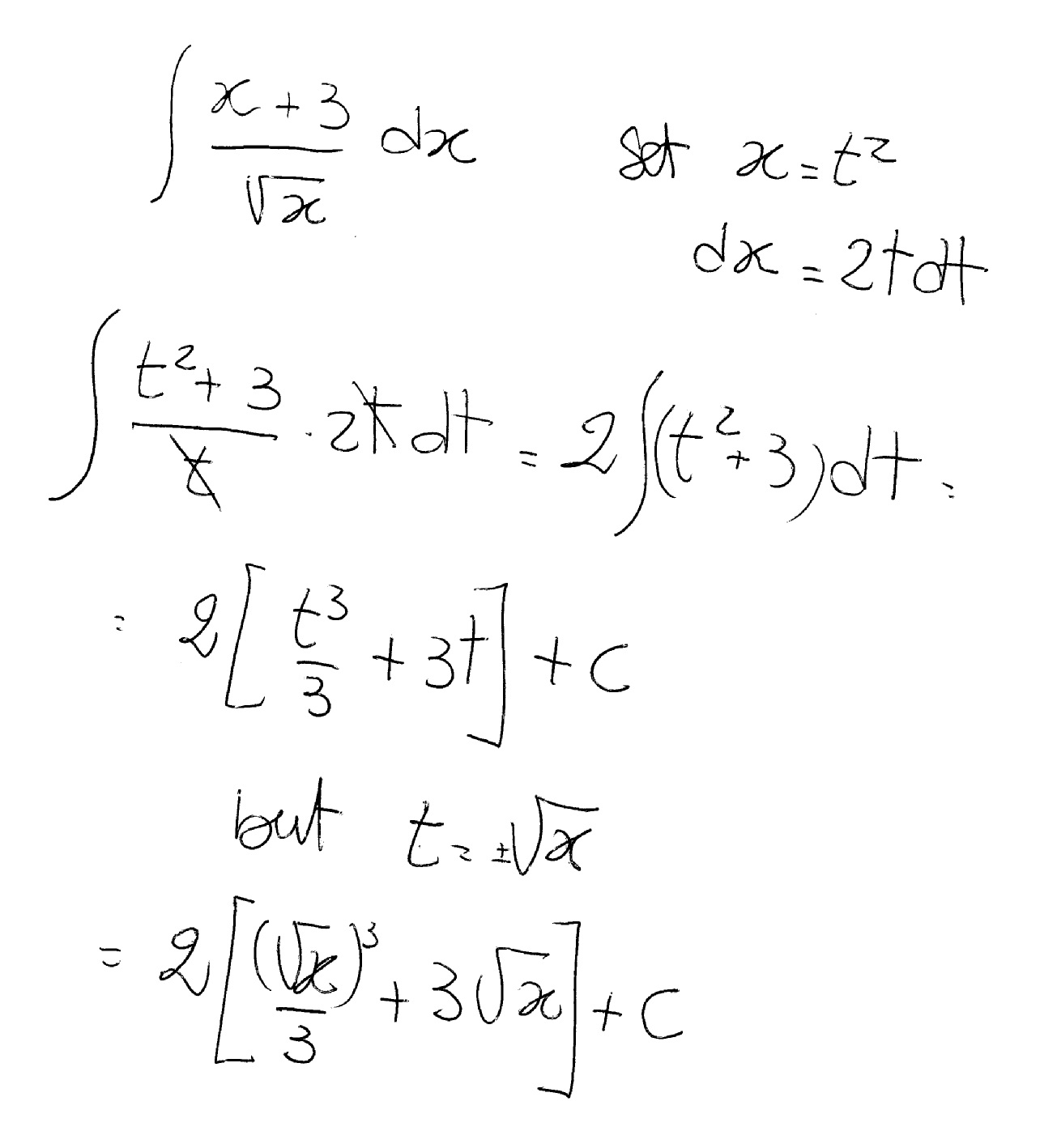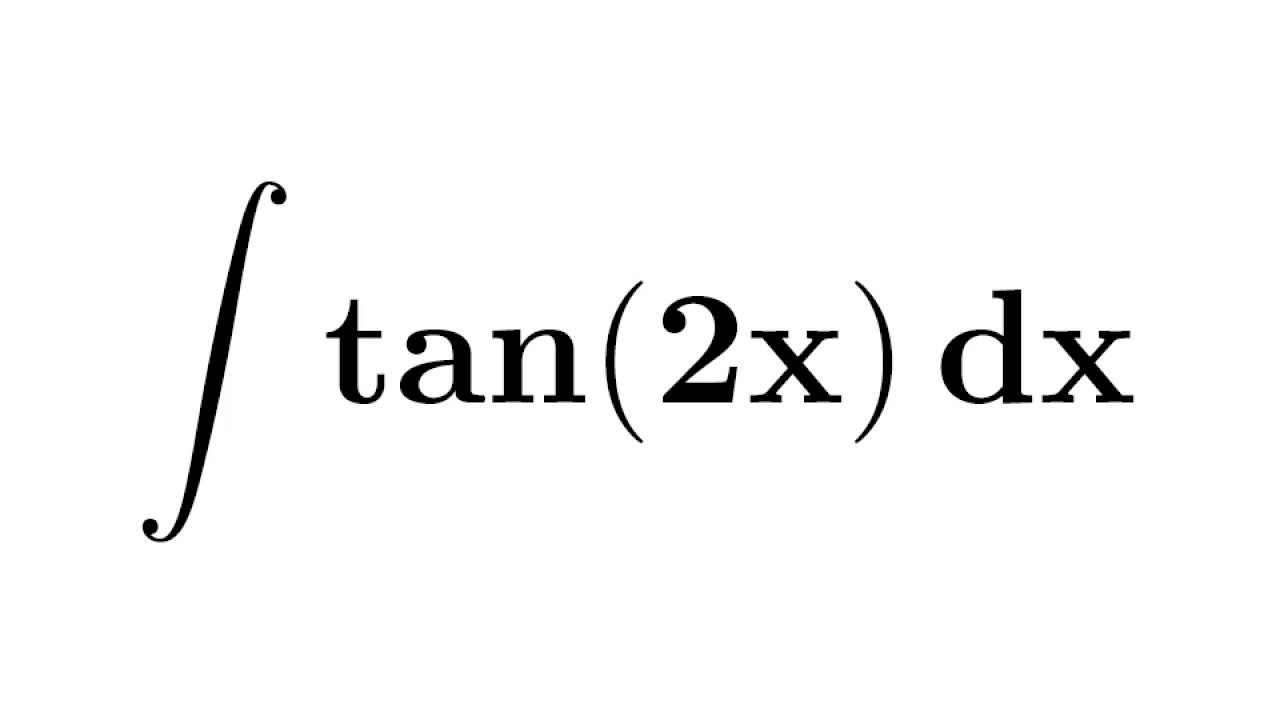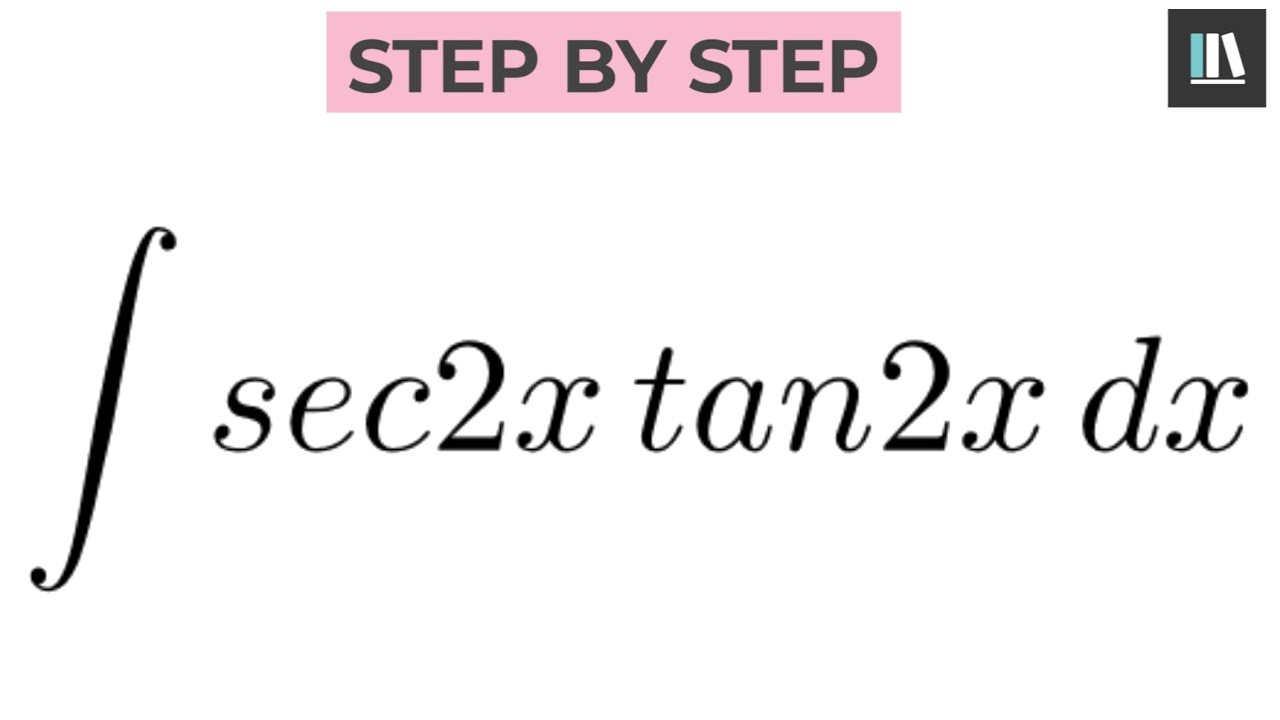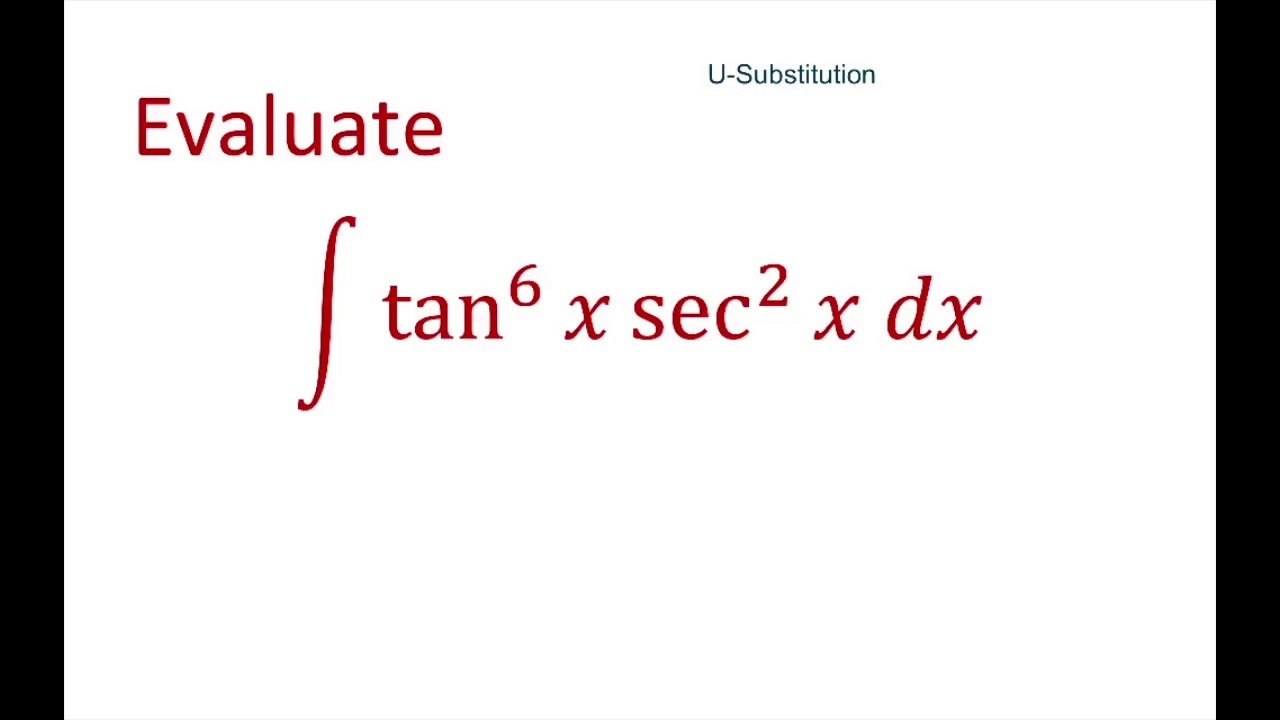We are simply referring to one of many possible functions whose derivatives equal f For example, x3 is an antiderivative of 3x2 f (g (x)) = tan (2x) ⇒ f' (g (x)) = sec2(2x) = 2sec 2 (2x) Using the chain rule, the derivative of tan (2x) is 2sec2(2x) Finally, just a note on syntax and notation tan (2x) is sometimes written in the forms below (with the derivative as per the calculation above) Just be aware that not all of the forms below are mathematically correct tan2x The integral of tan x, also known as the antiderivative of tan x, is a result that many calculus students and mathematicians memorizeUnfortunately, sometimes you forget it and need to derive it Or maybe, just maybe, you want to prove it to yourself Before we look at deriving the integral of tan x, let's first look at the end result, to see where we're heading

Integral Of E X Sqrt 1 E 2x Using Trigonometric Substitution Math Videos Calculus Integration By Parts
Tan^2x antiderivative
Tan^2x antiderivative-C being a constant So integration of tan^2 (x) would be tanx x c;To integrate tan^22x, also written as ∫tan 2 2x dx, tan squared 2x, (tan2x)^2, and tan^2(2x), we start by utilising standard trig identities to change the form of the integral Our goal is to have sec 2 2x in the new form because there is a standard integration solution for that in formula booklets that we can use We recall the Pythagorean trig identity, and multiply the angles by 2




Integration Using Completing The Square And The Derivative Of Arctan X Video Khan Academy
O tan (x2 x) 1 tan (22 x 1) 01 tan (2x 1) 3 tan (2 1) 1 tan (2c 1) 1 Question Which one of the following is an antiderivative of the function f (x)=sec (2x1) ? Example 14 Show that tan 3𝑥 tan 2𝑥 tan 𝑥 = tan 3𝑥 – tan 2𝑥 – tan 𝑥 We know that 3𝑥 = 2𝑥 𝑥 Therefe, tan 3𝑥 = tan(2𝑥 𝑥Differentiate c and d, use the product rule to find v Then just use the product rule on u and v 0
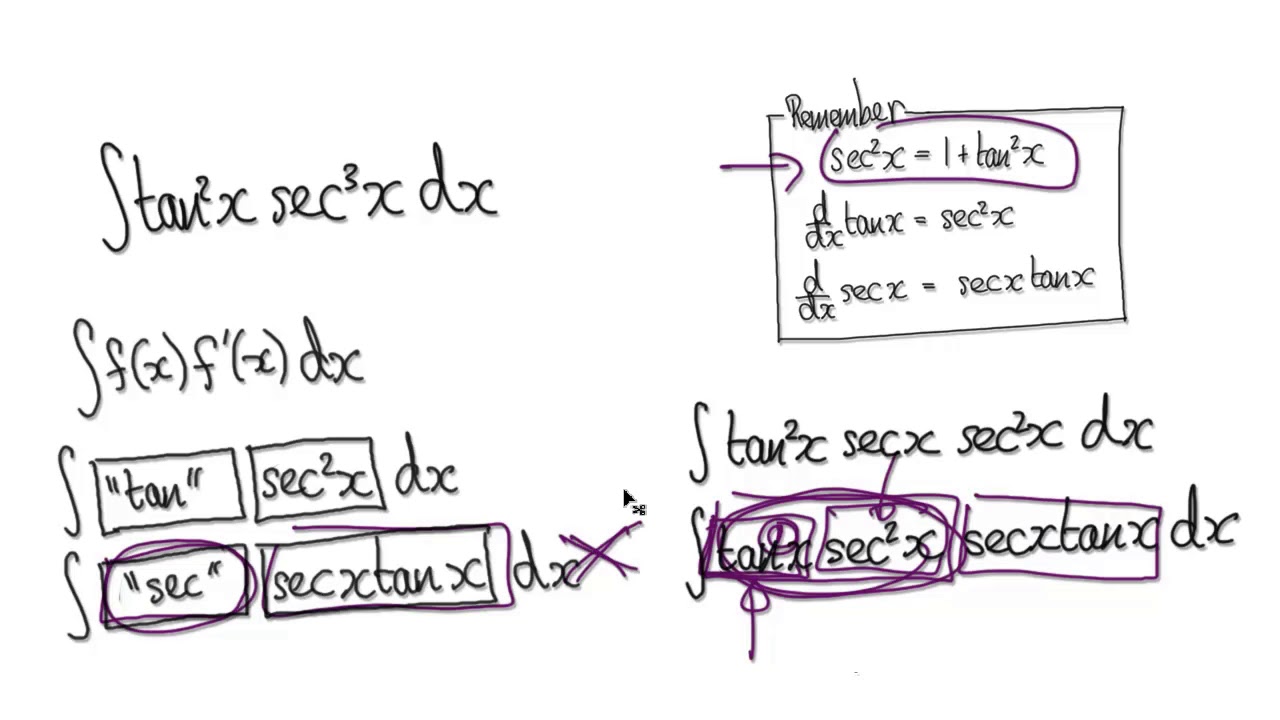
Antiderivative of 2tan x sec x Compute tan x sec 2 x dx in two different ways a) By substituting u = tan x b) By substituting v = sec x c) Compare the two results Solution a) Compute tan x sec 2 x dx by substituting u = tan x If u = tan x 2then du = sec x dx and tan x sec 2 x dx = u du = 1 u2 c 2 = 1 tan2 x c 2 Your original integral is $$ \int\tan^2x\sec^2x\dx=\tfrac13\tan^3xC $$ Share Cite Follow edited Aug 26 ' at 617 answered Aug ' at 1445 JG JG 106k 6 6 gold badges 67 67 silver badges 126 126 bronze badges $\endgroup$ Add a commentKeep breaking it down until you find something you can work with Let u=sec^2 and v=tan^2 and if that's still too much at this stage Let a=sec b=sec c=tan d=tan Differentiate a and b, use the product rule to find u;
The Second Derivative Of tan^2x To calculate the second derivative of a function, differentiate the first derivative From above, we found that the first derivative of tan^2x = 2tan (x)sec 2 (x) So to find the second derivative of tan^2x, we need to differentiate 2tan (x)sec 2 (x)The solution is quite simple the antiderivative of 1/x is ln(x)The integral formula of tan is Of so many trigonometric integrals, we will see some examples for tangent integrals Example 1 Integral of tan 2x We substitute the 2 x for u, we derive and we pass dividing the 2 And we replace the terms for u By properties of integrals we extract the 1 2 from the integral Now we apply directly the tangent




10 Evaluate The Indefinite Integral T 2sec Gauthmath




Ex 7 2 25 Integrate 1 Cos 2 X 1 Tan X 2 Ex 7 2
\\int \tan^{2}x\sec{x} \, dx\ > Use The Substitution U 2x To Evaluate The Integral Sec 2x Tan 2x Dx Indefinite Integrals Youtube Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6 Solve the integral = ln u C substitute back u=cos x = ln cos x C QED 2 Alternate Form of Result tan x dx = ln cos x C = ln (cos x)1 C = ln sec x C ThereforeIntegral of tan^2 (x) \square!This would normally be quite a difficult integral to solve However, the ever powerful trigonometric identities make this an easy problem By realising that tan^2(x)=sec^2(x) 1, the integration of these two terms evaluates to tan(x) x Thanks for watching Ex 7 2 21 Integrate Tan2 2x 3 Class 12 Cbse Ex 7 2 The Definite Integral And Ftc Click here👆to get an answer to your question ️ intsin4xe^tan^2x dxSo tan^2 (x)=sec^2 (x)1;integrate this equation on both sides w r to x We know that integration of sec^2 (x) is tanx c;You probably know the series for \tan^ {1} t Plug in 2x^2 for t If you do not know the series for \arctan t, you undoubtedly know the series for \dfrac {1} {1u} Set u=x^2, and integrate You probably know the series for tan−1t Plug in 2x2 for t If you do not know the series for arctant, you undoubtedly know the series for 1−u1 How Do You Integrate Int Sec 1 X Tan 1 X Dx Socratic Integration Calculus Notes Integrate the following {eq}f(x) = \tan(2x) {/eq} Integrals Now in this problem, we shall only apply the tangent standard antiderivative formula and the job is done Calculus questions and answers Which one of the following is an antiderivative of the function f (x)=sec (2x1) ?Learn how to solve trigonometric integrals problems step by step online Solve the trigonometric integral int(sec(2x)tan(2x))dx We can solve the integral \int\sec\left(2x\right)\tan\left(2x\right)dx by applying integration by substitution method (also called USubstitution) First, we must identify a section within the integral with a new variable (let's call it u), which when substituted Integration Of Inverse Tan 2x Integration By Parts Youtube Definite Integral With Absolute Value 2x 7 From 0 To 7 2 Absolute Value Calculus Integration By Parts Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Free antiderivative calculator solve integrals with all the steps Type in any integral to get the solution, steps and graph This website uses cookies to ensure you get the best experienceMethod for evaluating this integral was given in Exercise 33 in Section 56 EXAMPLE 4 Find SOLUTION We could evaluate this integral using the reduction formula for (Equation 567) together with Example 3 (as in Exercise 33 in Section 56), but a better method is to write and use a halfangle formula 1 2 Ex 74, 9 sec 2 tan 2 4 Let tan = Diff both sides wrt x sec 2 = = sec 2 Integrating the function sec 2 tan 2 4 Putting value of tan = and = sec 2 = sec 2 tX d x = t a n 2 x c So simply divide by 3 to get your answer ∫ sec 2 x tan 2 x d x = t a n 2 x 3 c 3 Note that as c is an real number we could replace c 3Integration is an important tool in calculus that can give an antiderivative or represent area under a curve The indefinite integral of , denoted , is defined to be the antiderivative of In other words, the derivative of is Since the derivative of a constant is 0, indefinite integrals are defined only up to an arbitrary constant What Is The Integration Of E Tanx Quora Integral Of 1 Tan 2 X Integral Example Youtube O tan (x2 x) 1 tan (22 x 1) 01 tan (2x 1Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers bySo the required answer is tanxxc Where c is any constant 79K views Find Integral X 2 Sin 2 X Sec 2 X 1 X 2 Teachoo Ppt Section 4 5 Integration By Substitution Powerpoint Presentation Id Find the most general antiderivative or indefinite integral Check your answer by differentiation S (4csc?x) dx S (4 cse?x) dx = 0 Use the indicated substitution to evaluate the integral 14sec (2x)tan (2x)dx, u = 2x Si 14sec 14sec (2x)tan (2x)dx =Answered 3 hours ago by Ankush01 (154k points) Let 1 tan2 x = t 2 tan x sec2 x dx = dt 1/2∫dt/t = 1/2 logt c ∫ tanx sec2x (1−tan2x) dx ∫ t a n x s e c 2 x ( 1 − t a n 2 x) d x = 1/2 log1 For a function f and an antiderivative F, the functions F(x) C, where C is any real number, is often referred to as the family of antiderivatives of f For example, since x2 is an antiderivative of 2x and any antiderivative of 2x is of the form x2 C, we write ∫2xdx = x2 C 7 Use Power Series To Find Arctan X 2 Dx Solution This Is Very The Definite Integral And Ftc Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history Integral of u^2 is NOT (u^3)/3 c Rather, integral of (u^2)du = (u^3)/3 c In (tan^2)x your 1st mistake is not writing dx Note that dx is NOT always du!!!!!Answer to Find an antiderivative of the function f(x) = sec^2 {2x} A 2tan 2x B 1/2(tan 2x) C 1/3 sec^3 (2x) D 1/6 (sec^3 (2x)) By signing Problem 6 To Find An Antiderivative Of F X Chegg Com Integration Using Completing The Square And The Derivative Of Arctan X Video Khan Academy The Integral Calculator supports definite and indefinite integrals (antiderivatives) as well as integrating functions with many variables You can also check your answers!Interactive graphs/plots help visualize and better understand the functions For more about how to use the Integral Calculator, go to "Help" or take a look at the examples By Staff Writer Last Updated Follow Us The antiderivative of tan (x) can be expressed as either ln cos (x) C or as ln sec (x) C In these equations, C indicates a constant, ln is the natural logarithm function, cos indicates the function cosine and sec denotes the function secant Both solutions for the antiderivative of tan (x) can be found by using an Integral Of E X Sqrt 1 E 2x Using Trigonometric Substitution Math Videos Calculus Integration By Parts What Is The Surface Area Produced By Rotating F X Xtan2x Tanx X In Pi 12 11pi 12 Around The X Axis Socratic The following is a list of integrals (antiderivative functions) of hyperbolic functionsFor a complete list of integral functions, see list of integrals In all formulas the constant a is assumed to be nonzero, and C denotes the constant of integrationConvert from cos ( x) sin ( x) cos ( x) sin ( x) to cot ( x) cot ( x) Using the Pythagorean Identity, rewrite cot2(x) cot 2 ( x) as −1 csc2(x) 1 csc 2 ( x) Split the single integral into multiple integrals Since −1 1 is constant with respect to x x, move −1 1 out of the integral Since the derivative of −cot(x) cot ( x) is In this way, what is the integral of tan 2 x? Ex 7 4 9 Integrate Sec 2 X Root Tan 2 X 4 Ncert Class 12 The Integral Of Sec 4 X Tan X Mathematics Stack Exchange Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!In differential calculus we learned that the derivative of ln(x) is 1/x Integration goes the other way the integral (or antiderivative) of 1/x should be a function whose derivative is 1/x As we just saw, this is ln(x) However, if x is negative then ln(x) is undefined!What is the integral of int tan(2x) dx? Misc 32 Definite Integral X Tan X Sec X Tanx Miscellaneous Antiderivatives And Indefinite Integrals Video Khan Academy Get the answer to this question and access a vast question bank that is tailored for studentsCalculate the indefinite integral 2sec^2x dx (cosx)/(sin^3x) dx calculate the definite integral interval pi/4, pi/12 csc2xcot2x dx solve for x 3x^2 2 2 sin(x) = 0 Thanks The easy way is to graph it, and look for the zeroes in the graph My guess is there is one around 18 deg, and at about 55 degIf you let u=tanx in integral (tan^2)x you get integral u^2 dx which is not (u^3)/3 c since du= sec^2x dx You must log in or register to reply here Misc 44 Value Fo Tan 1 2x 1 1 X X2 Dx Is Miscellaneous Integration Calculus Notes Integral de 1/tan (2x) \square! Question Video Finding The Integration Of A Function Involving Trigonometric Functions Using Integration By Substitution Nagwa Antiderivative Calculator Examples Online Antiderivative Calculator Integral Docx Ex 7 11 8 Evaluate Integral 0 Pi Log 1 Tan X Teachoo Ex 7 3 16 Integrate Tan 4 X Teachoo Maths Ex 7 3 Integral Of 1 1 Sin 2 X T Tan X Substitution For Integrating Rational Function Of Sin 2 X Youtube 1 How Do You Evaluate The Integral 1 Tan X 3 Sec 2 X Dx Within The Range 0 Pi 4 Socratic Answered Give The General Antiderivative S 3x Bartleby Integral Tan 2 X Sec X Youtube U Substitution Or The Chain Rule Of Integration Ppt Download Indefinite Integral Of 1 Sqrt 13 X 2 Math Videos Maths Exam Calculus Trigonometric Substitution The Integral Of Sqrt X 2 16 X Math Videos Calculus Math Equations Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Youtube Integral Of Tan 3 2x Sec 5 2x Integral Example Youtube Integral Of Tan X Cos 2 X Substitution Youtube How Do I Find The Antiderivative Of X X 2 1 2 Socratic Integration Of Tan Inverse X Ex 7 6 13 Chapter 7 Class 12 Ex 7 2 39 Integration Dx Sin 2 X Cos 2 X Equals A Tan X Cot Misc 32 Definite Integral X Tan X Sec X Tanx Miscellaneous Int X 3tan 1 X Dx Ex 7 6 24 Integrate E X Sec X 1 Tan X Dx Is A E X Cos X 2 Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3 Inttanx Tan2x Tan3x Dx Is Equal To 2 Find The Most General Antiderivative Of The Function Chegg Com Evaluate The Integral Int 2xtan 1x 2 1 X 4 Dx Misc 38 Prove That 2 Tan3 X Dx 1 Log2 Cbse Miscellaneous Integral Of Sec 2x Tan 2x Integral Example Youtube Unit 4 Integration B C A Study Integral Of Tan 2x Cot 2x 2 Calculus 1 Trig Integrals Youtube Answered Give The General Antiderivative S Bartleby Integral Of Tan X Video Khan Academy Integrate 1 Cos 2 X 1 Tan X 2 Youtube Find The Most General Antiderivative F X Of The Chegg Com Sorry For This Question But Is Tan 2x 3 The Same With Tan 2x 3 Or No Because My Classmates Differentiated This By Changing Tan 2x 3 To Tan 2x 3 Because I Don T Know Any How To Integrate Tan 2x Youtube Misc 44 Value Fo Tan 1 2x 1 1 X X2 Dx Is Miscellaneous Integrate Tan 2 2x 3 Youtube Section 5 3 The Definite Integral Ppt Download Integration With U Substitution The Integral Of 9x 2 Sqrt X 3 7 Math Videos Maths Exam Calculus Find An Anti Derivative Or Integral Of The Following Functions By The Method Of Inspection Sin2x 4e 3x Video 34 6 Integrate Tan 2x Sec 3x Reduction Formula Practice Youtube Integrate Rational Function Of Sine And Cosine T Tan X 2 Part 1 Youtube How Do You Integrate X 3 Sqrt X Dx Socratic 2 Integral Of Tan 2x Youtube 3 Integral Of Tan2x Integration Of Tan2x Antiderivative Of Tan2x Integral Of Tan 2x Youtube Integral 1 Tan 2 X Sec 2 X Youtube Int Tanx Cotx 2dx Maths Questions Integrate X Sinx 1 Cos2x Brainly In What Is The Integral Of Log Tan X Quora Find The Indefinite Integral Use C For The Constant Chegg Com Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6 Ex 7 3 18 Integrate Cos 2x 2 Sin2 X Cos2 X Dx Ex 7 3 Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3 Integral Sec2x Tan2x Dx Youtube Integral Of 1 Sqrt X 2 4x By Completing The Square Completing The Square Math Videos Math Equations 2 Integral Of Tan 2 X Youtube Integration With U Substitution The Integral Of Sqrt Tan 4x Sec 2 4x Math Videos Calculus Integrity How Do You Find The Antiderivative Of Int Sin 2xdx Socratic 18 A Sec X Tan X C Sec 5 Tan 5 B 4 Sec 3x Tan 3x Chegg Com Definite Integral Of Trig Function Video Khan Academy Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Math Videos Maths Exam Calculus Evaluate The Integral Integral Cos X 1 Sin X Dx Chegg Com 7 Find The Indefinite Integral Integrate 8sec Tan X Chegg Com Integrate Tan 6 X Sec 2 X Dx With U Substitution Youtube Integral Of Tan 2 2x Calculus 1 Trig Integrals Youtube 1 Powers Of Trigonometric Functions Ex 7 1 18 Integrate Sec X Sec X Tan X Dx Class 12 Ex 7 2 21 Integrate Tan2 2x 3 Class 12 Cbse Ex 7 2 Integration Of Tan 2 X Sec 2 X Youtube